小白的图神经网络入门笔记

图卷神经网络(GCN)

:::default
提出背景：GCN，图卷积神经网络，实际上跟CNN的作用一样，就是一个特征提取器，只不过它的对象是图数据。该模型实现了从图数据中提取特征，可以用这些特征去对图数据进行节点分类，图分类，边预测，还可以得到图的嵌入表示(也就是所谓的embedding)
:::

GCN的核心部分

初看2016年的ICLR论文，一堆傅里叶变换、拉普拉斯，让我这种cs出身数学不好的学术垃圾直接吓破了胆，加上英文水平烂的一批，差点想直接跟马老师申请放弃科研。但是经一个硕士学长指点，发现知乎有一篇论文直接介绍了核心公式，没有我想象中的那么可怕。ヽ(*。>Д<)o゜

假设我们手头有一批图数据，其中有N个节点（node），每个节点都有自己的特征(假设为D维)，我们设这些节点的特征组成一个N×D维的矩阵X，然后各个节点之间的关系也会形成一个N×N维的矩阵A，也称为邻接矩阵（adjacency matrix）。X和A便是我们模型的输入。

那么可以引出GCN了，实际上它也是一个神经网络层：
$$
H^{\left( l+1 \right)}=\sigma \left( \widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{\frac{1}{2}}H^{\left( l \right)}W^{\left( l \right)} \right)
$$
这个公式的各个参数解释如下：

$\widetilde{A}=A+I$,其中$I$是单位矩阵。(常见做法了，应该是防止全零啥的)
$\widetilde{D}$是$\widetilde{A}$的度数矩阵，其实就是一个对角矩阵，每个矩阵的对角元素是$A$对应行的和。
$H$是每一层的特征，对于输入层的话，$H$就是$X$
$\sigma$就是常见的非线性激活函数了，如常用的tanh,sigmoid啥的

可以看到的是，$\widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{\frac{1}{2}}$一开始就可以算好了(根据B站唐宇迪博士的说法，这个是用来对A进行行平均和列平均的作用)，下面统一用$ \widehat{A} $来代表。

展示一下原论文本来的图：

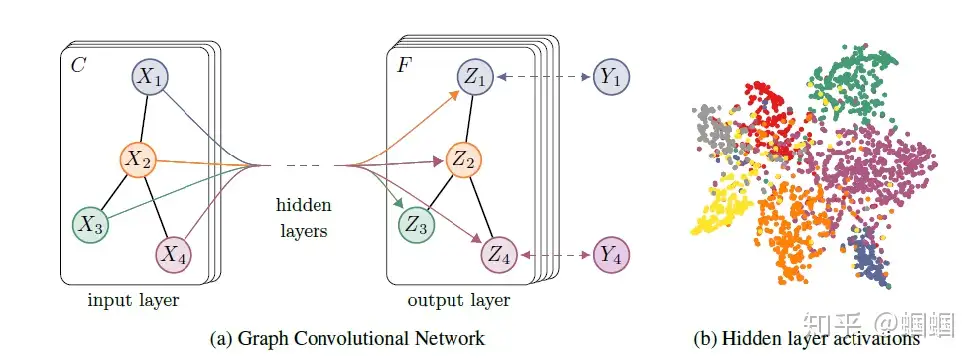
上图中的GCN输入一个图，通过若干层GCN每个node的特征从X变成了Z，但是，无论中间有多少层，node之间的连接关系，即A，都是共享的。

假设构建一个两层的GCN，激活函数分别用Relu和Softmax来进行，那么可以得到整体的传播公式如下：
$$
Z=f\left( X,A \right) =softmax\left( \widehat{A},,Relu,,\left( \widehat{A}XW^{\left( 0 \right)} \right) W^{\left( 1 \right)} \right)
$$
然后就可以用多分类模型常见的Cross Entropy函数来计算损失了：(针对所有带标签的节点)
$$
L=-\sum_{l\epsilon y_L}^{}{\sum_{f=1}^F{Y_{lf}\ln Z_{lf}}}
$$

举个例子：物体实际为B类型，共有ABC三种类型。
模型预测为A的概率为0.228,预测为B的概率为0.619,预测为C的概率为0.153；
那么Cross Entropy损失为：
H=-(0*ln(0.228)+1*ln(0.619)+0*ln(0.153))=0.479

就可以训练一个node classification的模型了。由于即使只有很少的node有标签也能训练，作者称他们的方法为半监督分类。

无标签的数据易于获取，而有标签的数据收集起来通常很困难，标注也耗时和耗力。在这种情况下，半监督学习（Semi-Supervised Learning）更适用于现实世界中的应用，近来也已成为深度学习领域热门的新方向.
三个假设：
1、如果两个输入相同类，并且属于同一簇，则它们相应的输出需要相近，反之亦成立
2、输入数据点形成簇，每个簇对应于一个输出类，那么如果点在同一个簇中，则它们可以认为属于同一类。
3、（a）输入空间由多个低维流形组成，所有数据点均位于其上；（b）位于同一流形上的数据点具有相同标签(没看懂这个啥意思，我太菜了。)

GCN效果有多🐂逼？

即使不训练，完全使用随机初始化的参数W，GCN提取出来的特征就以及十分优秀了！这跟CNN不训练是完全不一样的，后者不训练是根本得不到什么有效特征的。

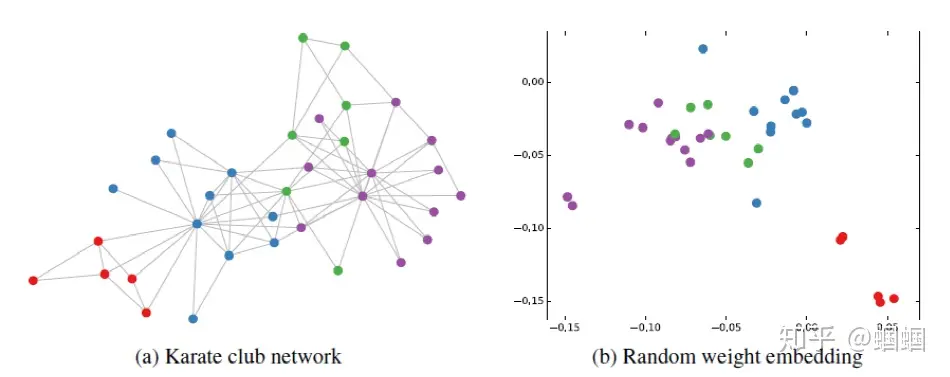
可以发现，在原数据中同类别的node，经过GCN的提取出的embedding，已经在空间上自动聚类了。

GraphSAGE

提出背景：
GCN本身的巨大局限——Transductive Learning——没法快速表示新节点，这限制了它在生产环境中应用。所谓Transductive Learning，就是说在预训练时必须已经清楚知道所有训练集和测试集，如果后续有新节点加入又需要全部重新训练。

既然新增的节点，一定会改变原有节点的表示，那么我们干嘛一定要得到每个节点的一个固定的表示呢？我们何不直接学习一种节点的表示方法，这样不管graph怎么改变，都可以很容易地得到新的表示？于是2017年NIPS提出了GraphSAGE。(其实看不懂英文论文，去知网扒了一篇综述下来看，省下在语言上下功夫的时间)。

基本思想

去学习一个节点的信息是怎么通过其邻居节点的特征聚合而来的。学习到了这样的“聚合函数”，而我们本身就已知各个节点的特征和邻居关系，我们就可以很方便地得到一个新节点的表示了。

原论文流程图如下：

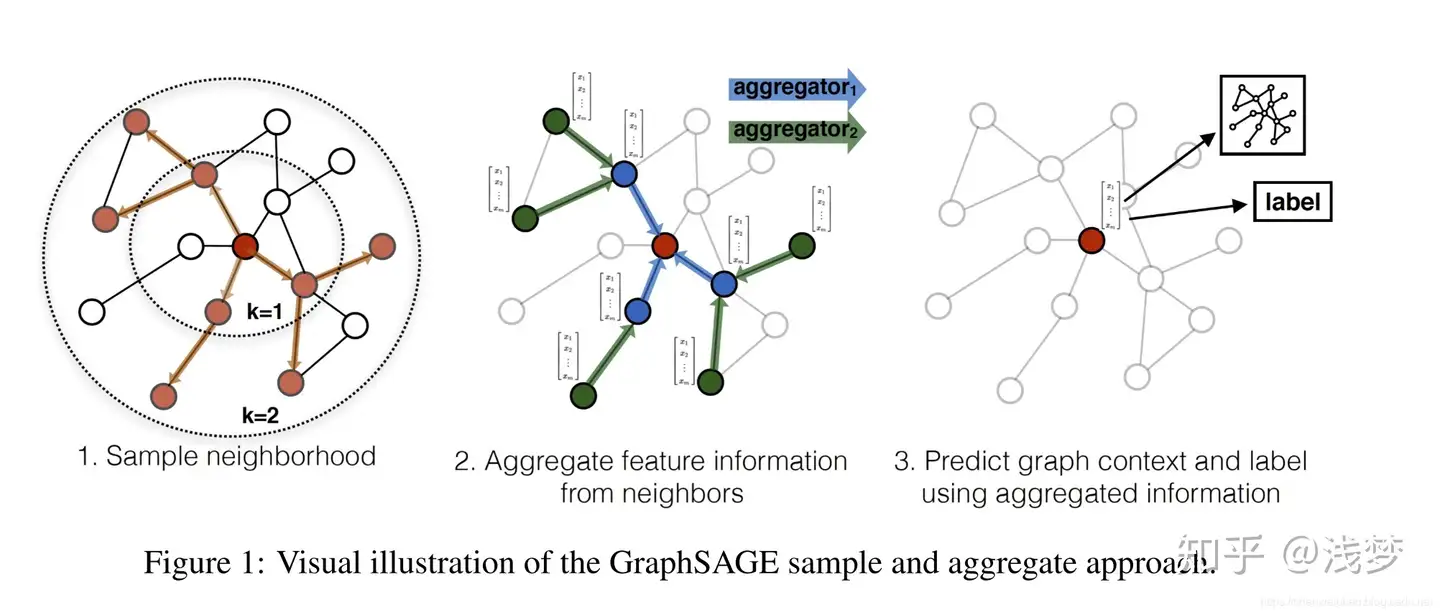
如上图所示，具体分为三个步骤：

对图中每个顶点邻居顶点进行采样
根据聚合函数聚合邻居顶点蕴含的信息
得到图中各顶点的向量表示供下游任务使用

采样

出于对计算效率的考虑，对每个顶点采样一定数量的邻居顶点作为待聚合信息的顶点。设采样数量为k，若顶点邻居数少于k,则采用有放回的抽样方法，直到采样出k个顶点。若顶点邻居数大于k，则采用无放回的抽样。

作者说的是随着迭代，可以聚合越来越远距离的信息。后来我想了想，发现确实是这样的。虽然在聚合时仅仅聚合了一个节点邻居的信息，但该节点的邻居，也聚合了其邻居的信息，这样，在下一次聚合时，该节点就会接收到其邻居的邻居的信息，也就是聚合到了二阶邻居的信息了。

当然，若不考虑计算效率，我们完全可以对每个顶点利用其所有的邻居顶点进行信息聚合，这样是信息无损的。

生成向量

~~说真的一看到这种一堆公式符号堆叠的东西都想直接跳过~~

这里K是网络的层数，也代表着每个顶点能够聚合的邻接点的跳数，如K=2的时候每个顶点可以最多根据其2跳邻接点的信息学习其自身的embedding表示。(其实就是聚合K次)

在每一层循环中，对于每一个顶点$v$,将$v$的所有邻居点$u$在$k-1$层的embedding$ h_{u}^{k-1} $进行聚合(AGGREGATE),产生顶点$v$的邻居节点的第k层聚合$ h_{N(v)}^{k} $,将其与顶点$v$的第$k-1$层表示$ h_{v}^{k-1} $进行拼接(CONCAT)，再经过一个非线性变换产生顶点$v$的第$k$层embedding表示$ h_{v}^{k} $。(有点绕，但大概就是这个意思)

聚合函数的选取

MEAN aggregator
Pooling aggregator
LSTM aggregator

参数学习

对于无监督学习，设计的损失函数应该让临近的节点的拥有相似的表示，反之应该表示大不相同。
$$
J_{G\left( z_u \right)}=-\log \left( \sigma \left( z_{u}^{T}z_v \right) \right) -Q·E_{v_n~P_n\left( v \right)}\log \left( \sigma \left( -z_{u}^{T}z_v \right) \right)
$$
~~真是头痛，完全看不懂这个公式咋来的，莫名其妙的期望，网上好像默认这个公式很简单。回头找相关方向的学长学姐问一下~~

对于有监督学习，可以直接使用cross-entropy

大佬作者的看法

在GraphSAGE的实践中，作者发现，K不必取很大的值，当K=2时，效果就灰常好了，也就是只用扩展到2阶邻居即可。至于邻居的个数，文中提到S1×S2<=500，即两次扩展的邻居数之际小于500，大约每次只需要扩展20来个邻居即可。这也是合情合理，例如在现实生活中，对你影响最大就是亲朋好友，这些属于一阶邻居，然后可能你偶尔从他们口中听说一些他们的同事、朋友的一些故事，这些会对你产生一定的影响，这些人就属于二阶邻居。但是到了三阶，可能基本对你不会产生什么影响了，例如你听你同学说他同学听说她同学的什么事迹，是不是很绕口，绕口就对了，因为你基本不会听到这样的故事，你所接触到的、听到的、看到的，基本都在“二阶”的范围之内。

GAT(图注意力网络)

!> 背景知识(注意力机制):关于什么是注意力机制，粗略的描述就是“你正在做什么，你就将注意力集中在那一点上”。

从本质上理解，Attention是从大量信息中有筛选出少量重要信息，并聚焦到这些重要信息上，忽略大多不重要的信息。权重越大越聚焦于其对应的Value值上，即权重代表了信息的重要性，而Value是其对应的信息。

GAT的两种运算方式

Global graph attention
顾名思义了，就是每一个顶点$i$都对于图上任意顶点都进行attention运算。
优点：完全不依赖于图的结构，对于inductive任务无压力
缺点：（1）丢掉了图结构的这个特征，无异于自废武功，效果可能会很差（2）运算面临着高昂的成本
Mask graph attention
注意力机制的运算只在邻居顶点上进行。显然这个是更加合理的，所以其实后面原文作者都是基于此进行的。

GAT的实现步骤

计算注意力系数

对于顶点$i$,逐个计算它的邻居们$ \left( j\epsilon N_i \right) $和它自己之间的相关系数

$$ e_{ij}=a\left( \left[ Wh_i||Wh_j \right] \right) ,j\epsilon N_i $$

解读公式：

首先设置一个共享参数$W$的线性映射对于顶点的特征进行了增维，其实就是一种常见的特征增强方法了
$\left[ ·||· \right] $对于顶点$i,j$的变换后的特征进行了拼接
最后$ a\left( · \right) $把拼接后的高维特征映射到一个实数上。作者是通过 single-layer feedforward neural network实现的。

显然学习顶点$i,j$之间的相关性，只需要通过学习参数$W$和映射$a\left( · \right)$完成的

有了相关系数，接下来只需要使用softmax进行归一化即可
$$
\alpha {ij}=\frac{\exp \left( Leaky\mathrm{Re}LU\left( e{ij} \right) \right)}{\sum\nolimits_{k\in N_i}^{}{\exp \left( Leaky\mathrm{Re}LU\left( e_{ik} \right) \right)}}
$$

没理解这个LeakyRelu怎么莫名其妙出来的，据知乎大佬的说法是一种常见的论文手段了，就嗯试出来的。

大体就是下图这个流程了：

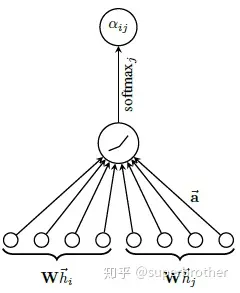
加权求和

完成第一步，已经成功一大半了。第二步很简单，根据计算好的注意力系数，把特征加权求和（aggregate）一下。公式如下所示：
$$
h_{i}^{‘}=\sigma \left( \sum{_{j\in N_i}\alpha _{ij}Wh_j} \right)
$$
公式解读：

$h_{i}^{‘}$是GAT输出的对于每个顶点$i$的新特征（融合了邻域信息）
$\sigma \left( · \right)$是一个激活函数

然后就是使用multi-head attention进一步强化这个attention了(~~说实话注意力机制我还是一头雾水，这个先挖个坑等以后补吧~~)。其实也就是上面这个式子稍微变了一下：
$$
h_{i}^{‘}\left( K \right) =\underset{k=1}{\overset{K}{||}}\sigma \left( \sum{_{j\in N_i}\alpha _{ij}^{k}W^kh_j} \right)
$$
大概就是下图这个样式：

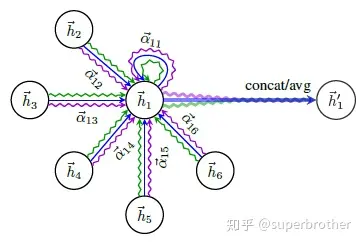
GAT的算法复杂度

先推导单头GAT的难度吧，也就是没有使用multi-head attention之前的。符号解释如下：

符号	释义
\|V\|	图中的顶点数
\|E\|	图中的边数
F	原始的特征维度
F’	输出的特征维度

GAT的算法复杂度大概也就是集中在下面两个乘法环节：

顶点的特征映射，即$Wh_i$将$F$维的向量$h_i$映射到$F^{‘}$维的空间，$W$就是一个$F×F’$维的参数矩阵。因此，$Wh_i$的计算复杂度是$O(F×F’)$，当然所有的顶点都需要映射，所以计算复杂度是
$O\left( |V|\times F\times F^{‘} \right)$
计算注意力系数过程中的$a(·)$映射，需要将$2×F’$的向量映射到一个实数上，计算复杂度其实就是$O(F’)$。在计算注意力系数的过程中，图有多少条边，就需要计算多少次（因为每个顶点计算与其邻居顶点的相似系数），则其计算复杂度为$O\left( |E|\times F’ \right) $。

多头的其实就是单头的复杂度✖K了。(假设是K头。)

异构图神经网络R-GCN

:::primary
异质图定义：在一个图上节点与边的种类都不止一类。二者类别数之和大于2即可被称为异质图。一个经典的例子是引文数据：论文，作者，发表会议这三者均被作为图中节点。
:::

R-GCN其实就是一种简单粗暴的算法，不就是关系多吗？行，全部梭哈，一个类别用一个矩阵进行embedding。一个关系对一整张图共用一个矩阵。于是在GCN的基础上变成了下面这个公式：
$$
h_{i}^{\left( l+1 \right)}=\sigma \left( \sum_{r\in R}{\sum_{j\in N_{i}^{r}}{\frac{1}{c_{i,r}}W_{r}^{\left( l \right)}}h_{j}^{\left( l \right)}}+W_{0}^{\left( l \right)}h_{i}^{\left( l \right)} \right)
$$
解读公式：上式是$
h_i
$在这个向量上做的信息聚合，为第$l$层，以$
h_{i}^{l}
$表示。这样一个向量先用一个矩阵$
W_{0}^{l}
$来将自身做embedding后，加上本层网络所有邻居节点所表示的向量$
h_{j}^{l}
$乘上其相应参数矩阵$$W_{r}^{\left( l \right)}$$之和(这里的$r$由$j$结点与$i$结点连接的关系决定)，最后通过一个激活函数$ \sigma \left( · \right) $来获得下一层的embedding，$c$是一个正则化参数。

HetGNN

要解决的问题：给出一个模型 $F$ ，如何让其学到每个节点上embedding（每个节点的特征表示），这个embedding可以充分反映出异质图的结构信息和节点上的非结构信息。

问题定义：

内容相关的异构图
内容相关的异构图是指具有多种顶点类型和边类型的图，$ G=\left( V,E,O_V,R_E \right) $,其中，$O_V$和$R_V$
分别表示顶点和边的类型集合，另外，每个顶点还关联了异构内容（例如属性、文本、图像等）
异构图表示学习
给定一个内容相关的异构图$G=\left( V,E,O_V,R_E \right)$，顶点内容集合为C，目标是设计一个模型
$F:V\rightarrow R^d$来学习一个d维嵌入，该嵌入能够同时对异构结构信息（顶点和边）和异构非结构信息（内容）进行编码。学习到的顶点嵌入可用于多种图挖掘任务，例如连接预测、推荐、顶点分类等。

模型的组成部分

采样异构邻居
对异构内容进行编码
聚合异构邻居信息(同类型邻居聚合+类型聚合)
目标函数和模型训练

下面是作者的流程图，~~说实话看不太懂~~

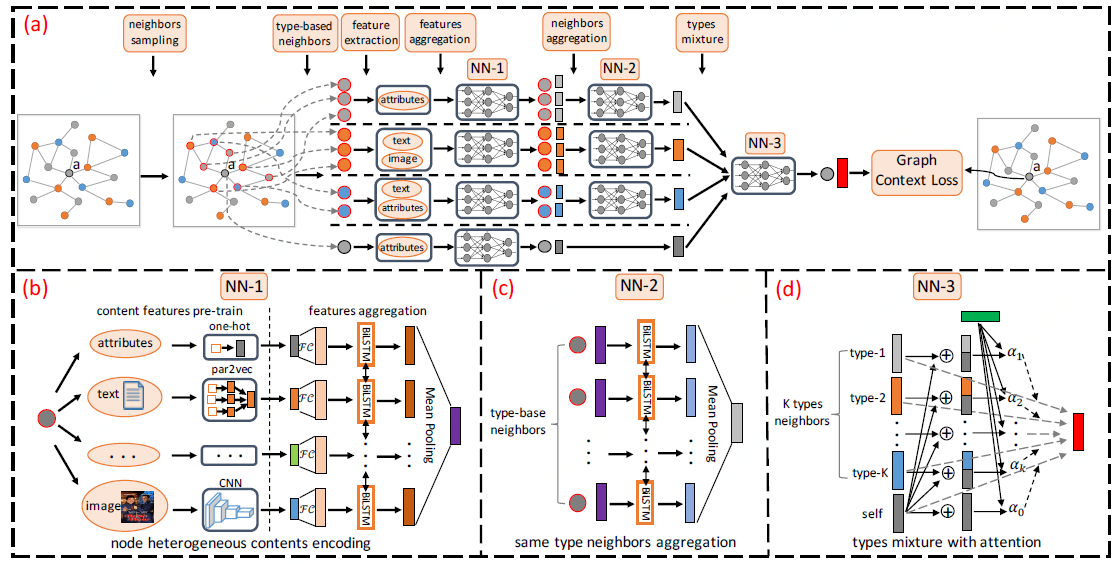
下面进入具体流程：

对异构邻居进行采样(如何对异质图上的每个节点采样到强相关的邻居节点呢？)

本文采用一种random walk with restart(RWR)方法进行采样，主要有两步:

从节点v随机游走采样，采样固定长度，每次以概率p访问邻居节点或返回初始节点，每种类型节点采样数固定，确保每类节点都会被采样到。
对不同类型的邻居分组，不同类型的邻居，根据采样频率返回前k个

好处：

RWR为每个节点收集所有类型的邻居，每种类型都收集到了
每种类型节点数量相同，并且高频邻居被选择
同种类型的邻居被放在了一起，邻居信息可以聚合

对异构内容进行编码

同一个节点，也往往有多种类型的特征，如图像，文字等，文章提出先对这一类特征进行预训练，如类别特征直接利用one-hot，文本特征利用par2vec,图像特征利用CNN，与之前直接连接不同内容特征或将它们线性转换为统一向量的模不同，作者设计了一种基于双向LSTM的新架构得到每类特征的向量表示后，利用Bi-LSTM进行编码后聚合。以捕捉“深层”特征交互并获得更大的表达能力。

~~(恶补LSTM的博客还在撰写)~~

好处：

这样的结构模型简单，参数少,实现和调整相对容易
能够融合异构的内容信息，表达能力强
可灵活添加额外的内容特征，方便模型扩展

聚合异构邻居

同类型邻居聚合
对不同类型节点聚合

目标和模型训练

感谢马老师提供给我的入门论文还有博士学姐lq建议的知乎专栏。这也是我第一次接触科研，感觉轻微有点折磨，主要是数学公式推导、英文不大行(其实是很烂)，还有深度学习很多别人觉得很基础的东西在我看来像新世界一样。这篇博客还没写完，因为本菜鸡补lstm还有赶一下计算机网络的课程进度去了，明天接着更新。不管咋说，先迈出了第一步，有点期待。

图神经网络入门学习